Executive Summary
Bitcoin and Ethereum both use elliptic-curve cryptography for generating keys and signing transactions. The algorithm they both use is called Elliptic Curve Digital Signature Algorithm (ECDSA), which represents a secure way of signing a message (a transaction for example) using Elliptic Curve Cryptography (ECC). This is a comparative analysis of BLS, Schnorr, and ECDSA signatures. The goal is to understand why are Ethereum and Bitcoin migrating from ECDSA, why BLS and Schnorr are superior to ECDSA and what are the key differences between them, how to use these signatures in the development and which Elliptic curves they are using and why.
Introduction
The main goal of this paper is to provide a clear understanding of the differences between them and how to use them in future protocol development; to understand why is Bitcoin migrating from ECDSA to Schnorr and why Ethereum is migrating from ECDSA to BLS.
Quick recap: ECDSA
Modern cryptography is founded on the idea that the key that you use to encrypt your data can be made public while the key that is used to to decrypt your data can be kept private. As such, these systems are known as public-key cryptographic systems.
ECDSA stands for Elliptic Curve Digital Signature Algorithm. Elliptic curve cryptography is a form of public key cryptography which is based on the algebraic structure of elliptic curves over finite fields. Used by both Bitcoin and Ethereum.
Elliptic curve: secp256k1
secp256k1
The elliptic curve domain parameters over Fp associated with a Koblitz curve secp256k1 are specified by the sextuple T = (p, a, b, G, n, h) where the finite field Fp is defined by:
- p =
0xFFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE FFFFFC2F=2^256 − 2^32 − 2^9 − 2^8 − 2^7 − 2^6 − 2^4 − 1
The curve E: y^2 = x^3 + ax + b over Fp is defined by:
- a =
0x00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 - b =
0x00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000007
The base point G in compressed form is:
0x02 79BE667E F9DCBBAC 55A06295 CE870B07 029BFCDB 2DCE28D9 59F2815B 16F81798
and in uncompressed form is:
0x04 79BE667E F9DCBBAC 55A06295 CE870B07 029BFCDB 2DCE28D9 59F2815B 16F81798 483ADA77 26A3C465 5DA4FBFC 0E1108A8 FD17B448 A6855419 9C47D08F FB10D4B8

Private and public keys
Private keys are generated as random 256 bits or 64 random hex characters or 32 random bytes. The public key is derived from the private key using ECDSA. Public key is a point on secp256k1 elliptic curve, generated by formula K = k * G where K is public key, k is private key, G is the constant point on secp256k1 elliptic curve and * is the multiplication operator on secp256k1 elliptic curve. There is no inverse, “/” operator, therefore the relationship between k and K is fixed, but can only be calculated in one direction, from k to K. A private key can be converted into a public key, but a public key cannot be converted back into a private key, because the math only works one way. The multiplication of k * G is equivalent to repeated addition, so G + G + G + … + G, repeated k times.
Signing and verification
To sign and verify ECDSA signature using OpenSSL, do next
# Generate private key
openssl genpkey -algorithm rsa -out privatni.pem
# Generate public key out of private key
openssl rsa -pubout -in privatni.pem -out javni.pem
# Test message for signing
echo "Test" > message.txt
# Sign the message (with Bitcoin's hashing alghorithm)
openssl dgst -sha256 -sign privatni.pem -out signature.bin message.txt
# Verification
openssl dgst -sha256 -verify javni.pem -signature signature.bin message.txt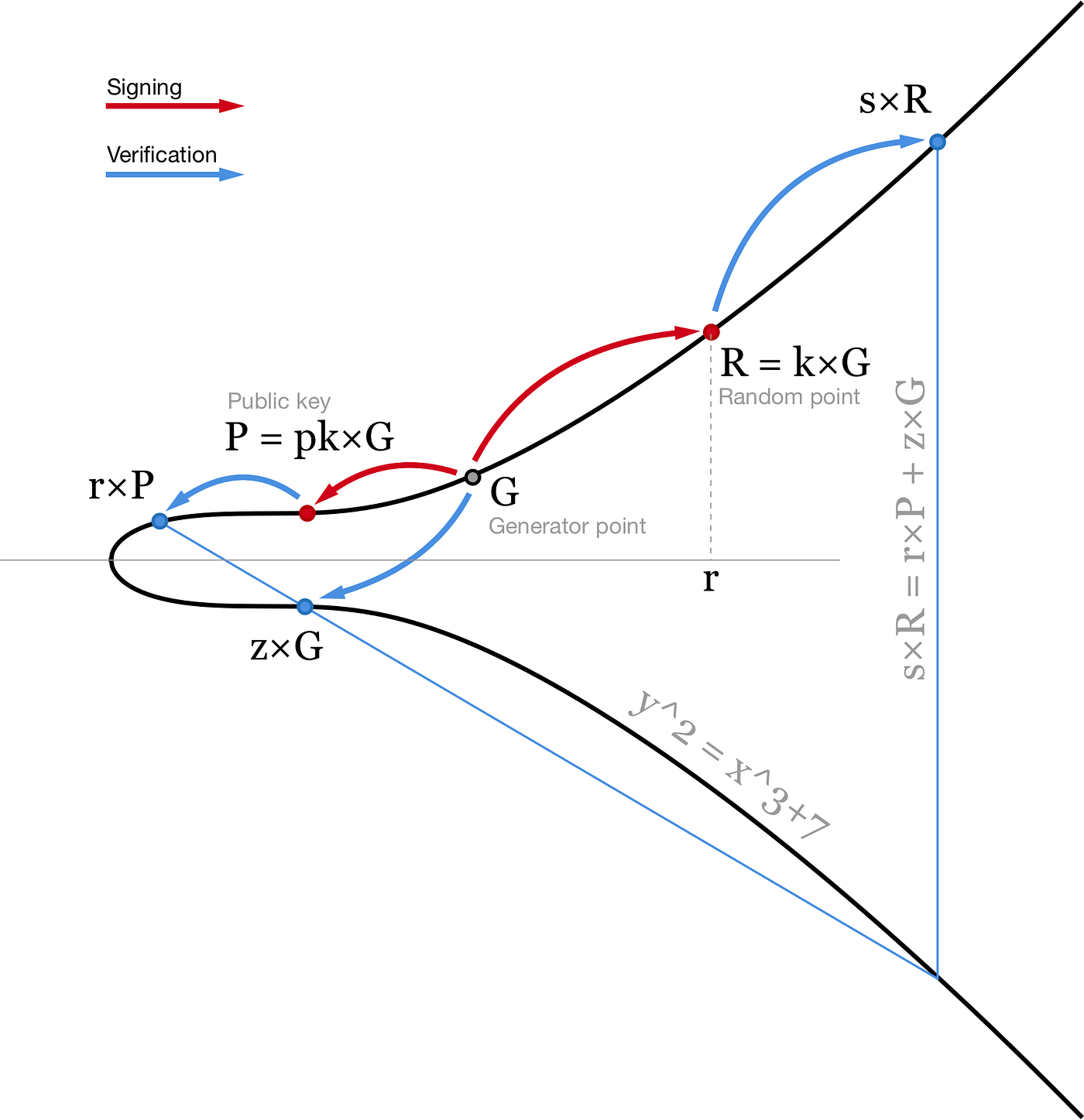
ECDSA verification in Solidity
import "@openzeppelin/contracts/utils/cryptography/ECDSA.sol";
contract Example {
address public admin;
constructor() {
admin = msg.sender;
}
function verify(bytes32 _digest, bytes calldata _signature) public view returns(bool) {
return admin == ECDSA.recover(_digest, _signature);
}
}ECDSA verification in Javascript/Typescript
import { SignerWithAddress } from '@nomiclabs/hardhat-ethers/signers';
import { utils } from 'ethers';
import { expect } from 'chai';
(async () => {
let admin: SignerWithAddress;
[admin] = await ethers.getSigners();
const message: string = 'Hello World';
const msgHash: string = utils.hashMessage(message);
const digest: Uint8Array = utils.arrayify(msgHash);
const signature: string = await admin.signMessage(message);
const address: string = utils.recoverAddress(digest, signature);
expect(address).to.equal(admin.address);
})();Goals & Methodology
BLS
BLS stands for Boneh-Lynn-Shacham, it’s a signature scheme that is based on bi-linear pairings. A pairing, defined as e(,), is a bilinear map of 2 groups G1 and G2 in some other group, GT. e(,) takes as arguments points in G1 and G2.
Pairings that verifies a signature looks like this:
e(g1, sig) = e(P, H(m))
# or in expanded form like this
e(g1, pk*H(m)) = e(pk*g1, H(m)) = e(g1, pk*H(m))H(m) is hashing a message to a point on an elliptic curve.
BLS consists of:
KeyGen — choose a random
α. Given generatorg1,P=α*g1Sign —
σ = α*H(m) ∈ G2(in the case of ETH 2.0)Verify
(P,m, σ)— ife(g1, σ) = e(P, H(m))returntrue.
Elliptic curve: BLS12-381
BLS12-381
BLS12-381 is a pairing-friendly elliptic curve construction that is optimal for zk-SNARKs at the 128-bit security level.
Barreto-Naehrig (BN) curves are a class of pairing-friendly elliptic curve constructions built over a base field Fp of order r, where r≈p. It is possible to construct a new BN curve that targets 128-bit security by selecting a curve closer to p≈2^(384). However, the larger group order r impairs the performance of multi-exponentiation, fast fourier transforms and other cryptographic operations.
Barreto-Lynn-Scott (BLS) curves are a slightly older class of pairing-friendly curves which now appear to be more useful for targeting this security level. Current research suggests that with p≈2^(384), and with an embedding degree of 12, these curves target the 128-bit security level.
Private and public keys
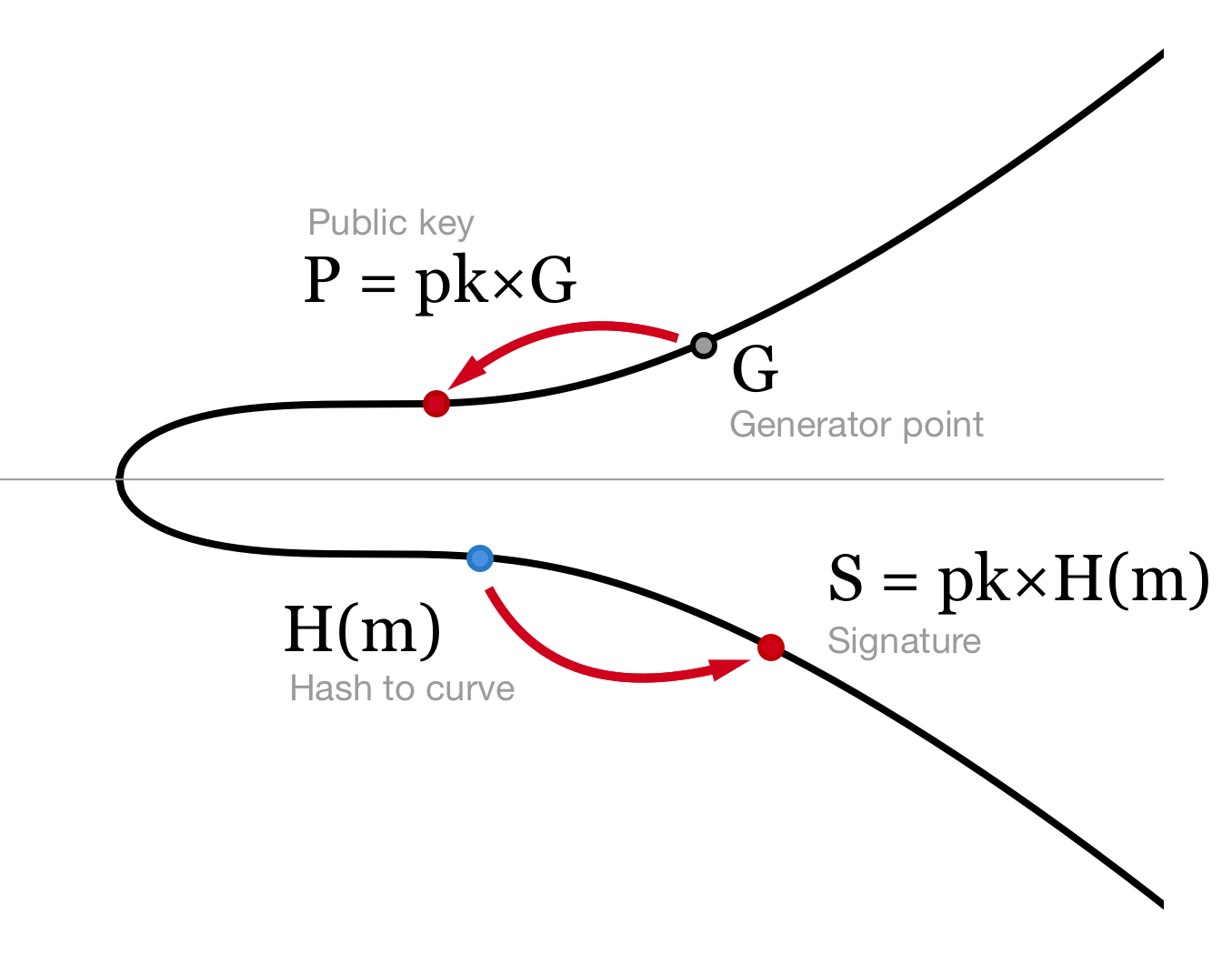
The private/secret key (to be used for signing) is just a randomly chosen number between 1 and r−1 inclusive. We’ll call it pk.
The corresponding public key is P=[pk]g1, where g1 is the chosen generator of G1. That is, g1 multiplied by pk, which is g1 added to itself pk times.
The discrete logarithm problem means that it is unfeasible to recover pk given the public key P.
Signing
One can sign the message by calculating the signature σ=[pk]H(m). That is, by multiplying the hash point by our secret key. But what is H?
To calculate a digital signature over a message, we first need to transform an arbitrary message (byte string) to a point on the G2 curve. The initial implementation in Eth2 was “hash-and-check”:
- Hash your message to an integer modulo
q - Check if there is a point on the curve with this
x-coordinate. If not, add one and repeat - Once you have a point on the curve multiply it by the
G2cofactor to convert it into a point inG2.
Verification
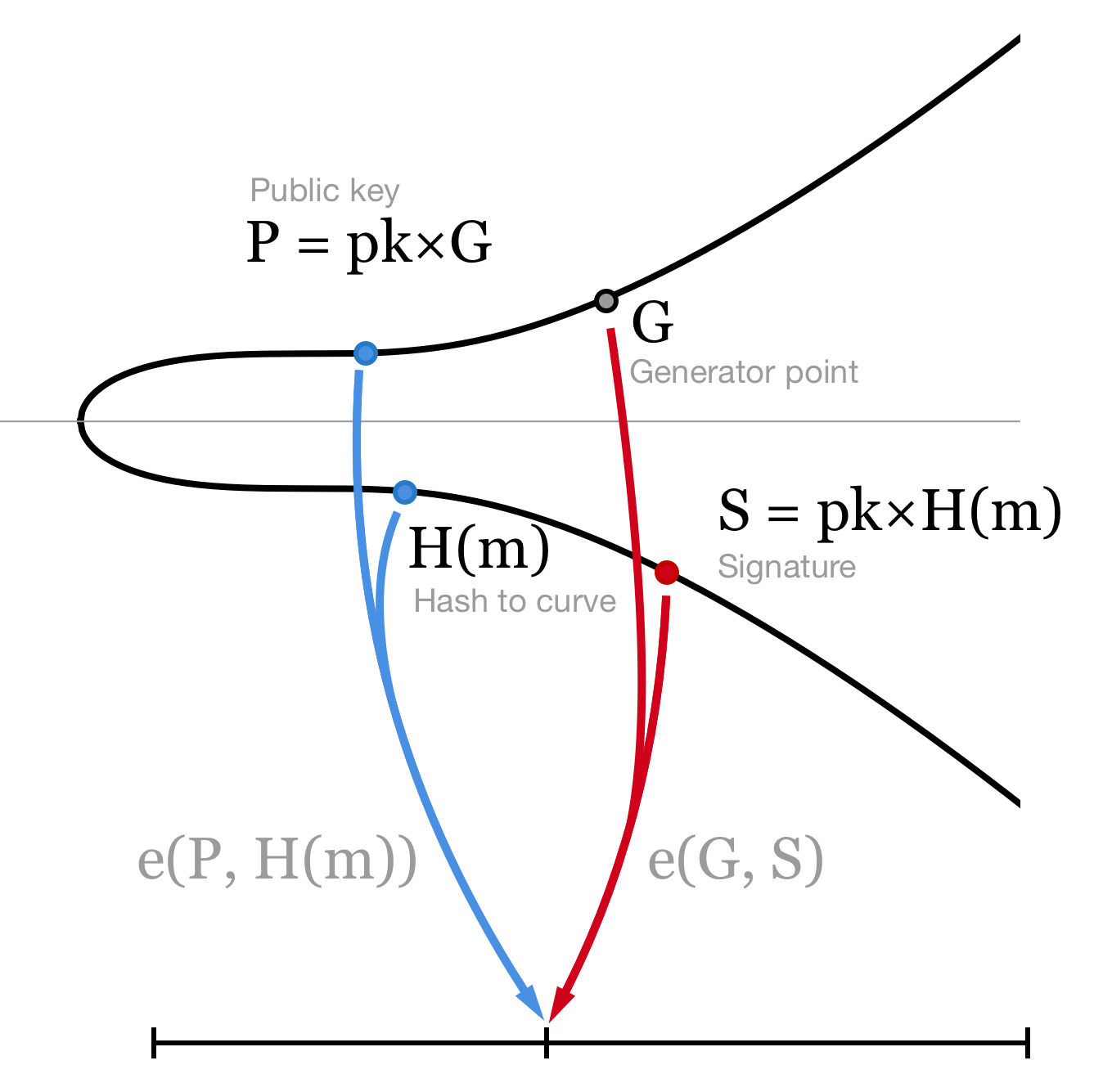
Given a message m, a signature σ, and a public key P, we want to verify that it was signed with the pk corresponding to P. The signature is valid if, and only if, e(g1,σ)=e(P,H(m)).
Aggregation
A really neat property of BLS signatures is that they can be aggregated, so that we need only two pairings to verify a single message signed by n parties, or n - 1 pairings to verify n different messages signed by n parties, rather than 2n pairings you might naively expect to need. Pairings are expensive to compute, so this is very attractive.
To aggregate signatures we just have to add up the G2 points they correspond to: σagg=σ1+σ2+...+σn. We also aggregate the corresponding G1 public key points Pagg=P1+P2+...+Pn.
Now the magic of pairings means that we can just verify that e(g1,σagg)=e(Pagg,H(m)) to verify all the signatures together with just two pairings.
BLS verification in Solidity
Below shows an example Solidity function that verifies a single signature. EIP-197 defined a pairing precompile contract at address 0x8 and requires input to a multiple of 192. This assembly code calls the precompile contract at address 0x8 with inputs.
// Negated genarator of G2
uint256 constant nG2x1 = 11559732032986387107991004021392285783925812861821192530917403151452391805634;
uint256 constant nG2x0 = 10857046999023057135944570762232829481370756359578518086990519993285655852781;
uint256 constant nG2y1 = 17805874995975841540914202342111839520379459829704422454583296818431106115052;
uint256 constant nG2y0 = 13392588948715843804641432497768002650278120570034223513918757245338268106653;
function verifySingle(
uint256[2] memory signature, \\ small signature
uint256[4] memory pubkey, \\ big public key: 96 bytes
uint256[2] memory message
) public view returns (bool) {
uint256[12] memory input = [
signature[0],
signature[1],
nG2x1,
nG2x0,
nG2y1,
nG2y0,
message[0],
message[1],
pubkey[1],
pubkey[0],
pubkey[3],
pubkey[2]
];
uint256[1] memory out;
bool success;
assembly {
success := staticcall(sub(gas(), 2000), 8, input, 384, out, 0x20)
switch success
case 0 {
invalid()
}
}
require(success, "");
return out[0] != 0;
}BLS verification in Javascript/Typescript
const bls = require('@noble/bls12-381');
(async () => {
// keys, messages & other inputs can be Uint8Arrays or hex strings
const privateKey =
'67d53f170b908cabb9eb326c3c337762d59289a8fec79f7bc9254b584b73265c';
const message = '64726e3da8';
const publicKey = bls.getPublicKey(privateKey);
const signature = await bls.sign(message, privateKey);
const isValid = await bls.verify(signature, message, publicKey);
console.log({ publicKey, signature, isValid });
// Sign 1 msg with 3 keys
const privateKeys = [
'18f020b98eb798752a50ed0563b079c125b0db5dd0b1060d1c1b47d4a193e1e4',
'ed69a8c50cf8c9836be3b67c7eeff416612d45ba39a5c099d48fa668bf558c9c',
'16ae669f3be7a2121e17d0c68c05a8f3d6bef21ec0f2315f1d7aec12484e4cf5',
];
const messages = ['d2', '0d98', '05caf3'];
const publicKeys = privateKeys.map(bls.getPublicKey);
const signatures2 = await Promise.all(
privateKeys.map((p) => bls.sign(message, p))
);
const aggPubKey2 = bls.aggregatePublicKeys(publicKeys);
const aggSignature2 = bls.aggregateSignatures(signatures2);
const isValid2 = await bls.verify(aggSignature2, message, aggPubKey2);
console.log({ signatures2, aggSignature2, isValid2 });
})();Schnorr
Schnorr signatures are generated slightly differently than ECDSA. Instead of two scalars (r,s) we use a point R and a scalar s. Similar to ECDSA, R is a random point on elliptic curve (R = k×G). Second part of the signature is calculated slightly differently: s = k + hash(P,R,m) ⋅ pk. Here pk is your private key, P = pk×G is your public key, m is the message. Then one can verify this signature by checking that s×G = R + hash(P,R,m)×P.
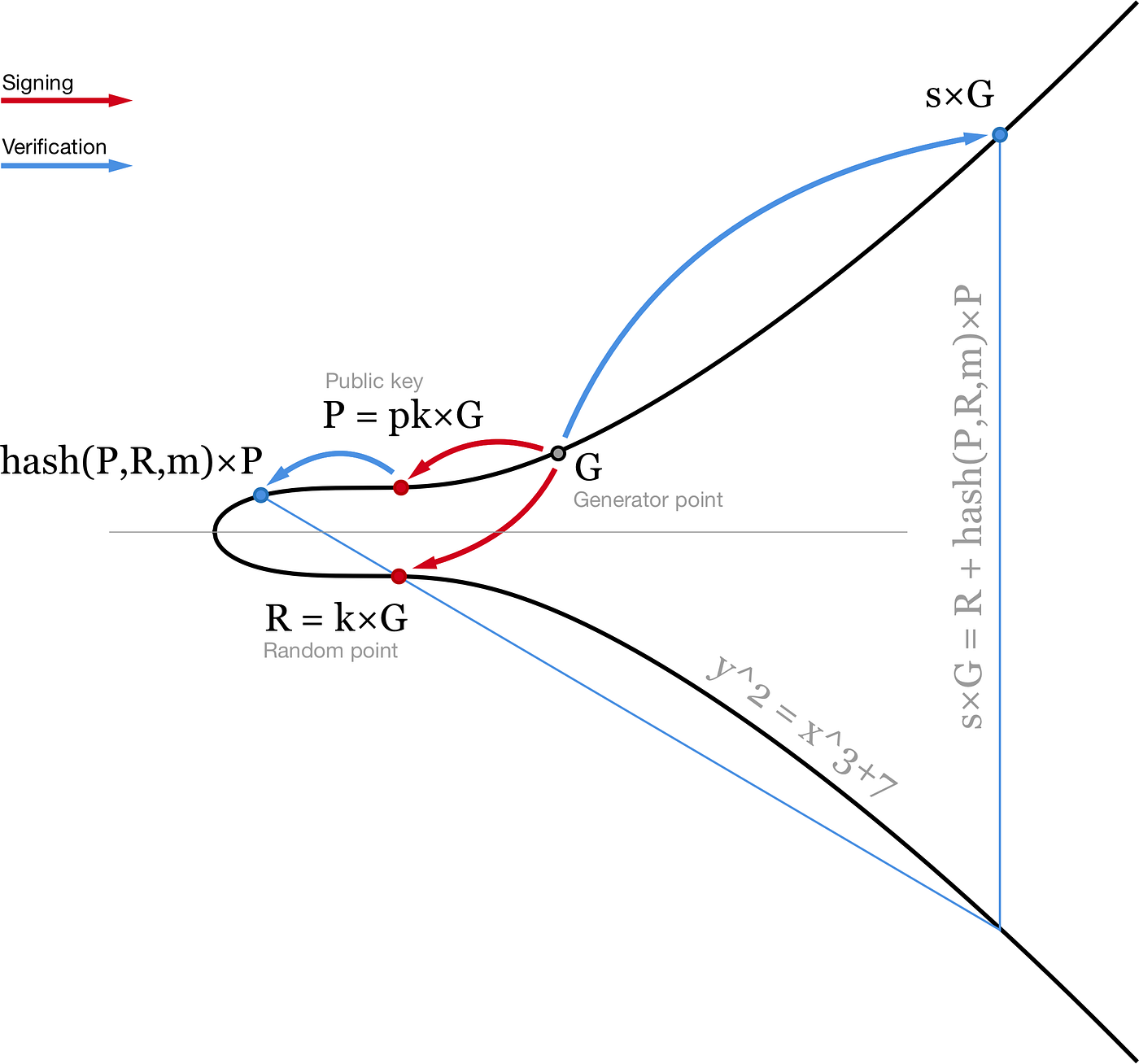
This equation is linear, so equations can be added and subtracted with each other and still stay valid. This brings us to several nice features of Schnorr signatures that we can use.
Batch validation
To verify a block in Bitcoin blockchain we need to make sure that all signatures in the block are valid. If one of them is not valid we don’t care which one - we just reject the whole block and that’s it.
With ECDSA every signature has to be verified separately. Meaning that if we have 1000 signatures in the block we will need to compute 1000 inversions and 2000 point multiplications. In total ~3000 heavy operations.
With Schnorr signatures we can add up all the signature verification equations and save some computational power. In total for a block with 1000 transactions we need to verify that
(s1+s2+…+s1000)×G=(R1+…+R1000)+(hash(P1,R1,m1)×P1+ hash(P2,R2,m2)×P2+…+hash(P1000,R1000,m1000)×P1000)Here we have a bunch of point additions (almost free in sense of computational power) and 1001 point multiplication. This is already a factor of 3 improvement - we need to compute roughly one heavy operation per signature.
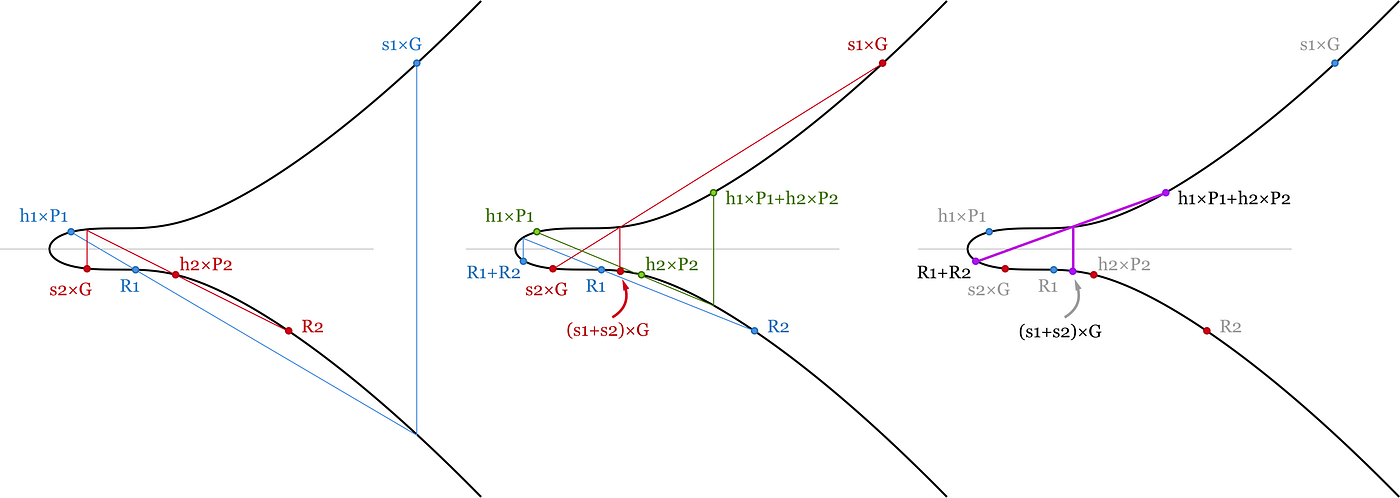
Key aggregation
We want to keep our bitcoins safe, so we might want to use at least two different private keys to control bitcoins. One we will use on a laptop or a phone and another one - on a hardware wallet / cold wallet. So when one of them is compromised we still have control over our bitcoins.
Currently it is implemented via 2-of-2 multisig script. This requires two separate signatures to be included in the transaction.
With Schnorr signatures we can use a pair of private keys (pk1,pk2) and generate a shared signature corresponding to a shared public key P=P1+P2=pk1×G+pk2×G. To generate this signature we need to choose a random number on every device (k1,k2), generate a random point Ri=ki×G, add them up to calculate a common hash(P,R1+R2,m) and then get s1 and s2 from every device (si = ki + hash(P,R,m) ⋅ pki). Then we can add up these signatures and use a pair (R, s) = (R1+R2, s1+s2) as our signature for shared public key P. No one else won’t be able to say if it is an aggregated signature or not - it looks exactly the same as a normal Schnorr signature.
Results & Discussion
A major reason to use this new stack is that it admits efficient aggregation of many signatures into one signature which directly contributes to the scalability of ETH2.0’s security. With this transition, ECDSA signatures aren’t enough anymore as the number of signatures to verify was too big and would take too long on the average machine.
ETH 2.0 definies 64 committees for every block and each committee can have as many as 2048 validators, with each epoch consisting of 32 blocks. Under normal ECDSA that means 131,072 (64*2048) signatures for every block (12 sec), and 4,194,304 for every epoch (32 blocks). This means that an epoch’s worth of signatures would be 33.6 megabytes which comes to ~7.6 gigabytes per day. In this case, all of the false claims about the ETH 1.0 state-size reaching 1TB back in 2018 would be true in ETH 2.0’s case in fewer than 133 days (based on signatures alone). If every node in the network will need to verify each signature it becomes infeasible to build a scalable, sharded, blockchain.
As a solution to the above, signature aggregation was considered. Technically it will mean that many signatures could be verified in a batch, significantly shortening the time and resources required. ETH 2.0 makes use of the BLS signatures - a signature scheme defined over several elliptic curves that is friendly to aggregation. On the specific curve chosen, signatures are 96 bytes each. If Alice produces signature A, and Bob’s signature is B on the same data, then both Alice’s and Bob’s signatures can be stored and checked together by only storing C = A + B. By using signature aggregation, only 1 signature needs to be stored and checked for the entire committee. This reduces the storage requirements to less than 2 megabytes per day.
Conclusion
It will be interesting to see how blockchain clients will implement these new changes and how efficient will they be because we already concluded from the paper that the reason for switching from ECDSA is justified. We should monitor also the Bitcoin timeframe to be able to disscus more about Schnoor signatures implementation.